-
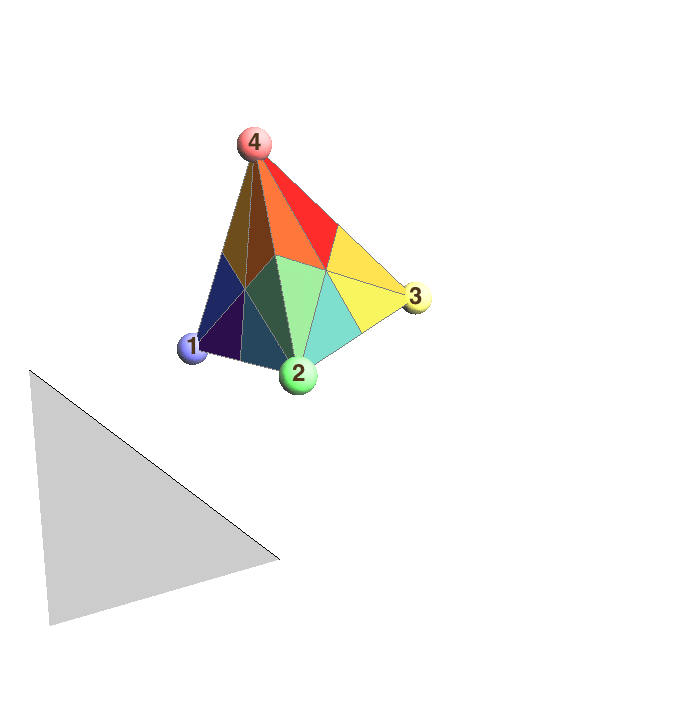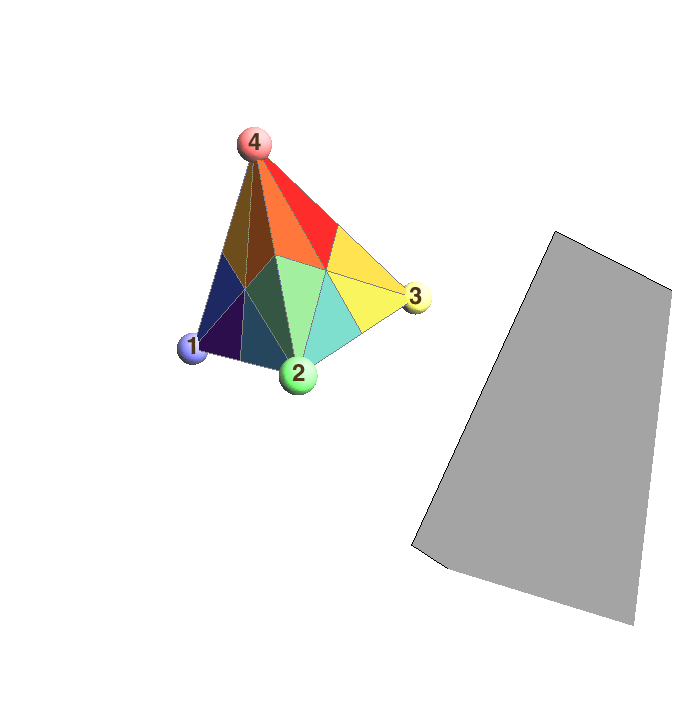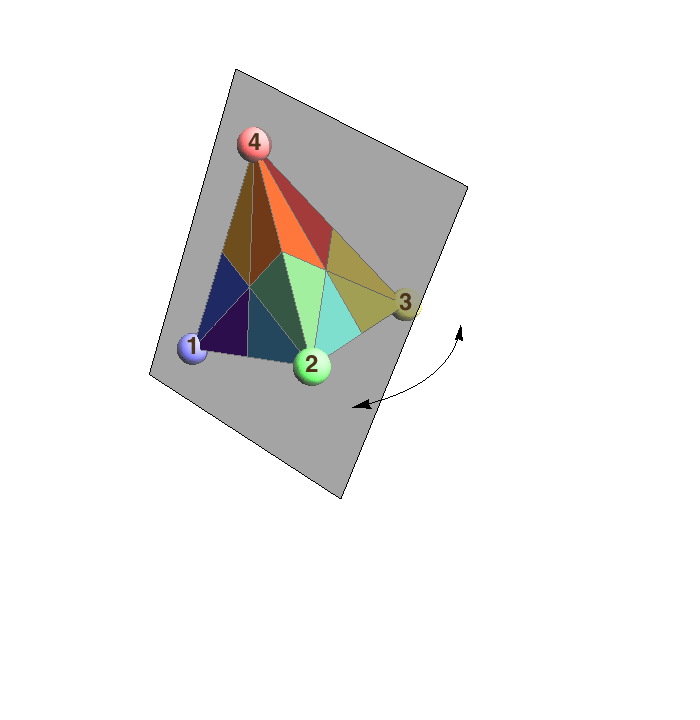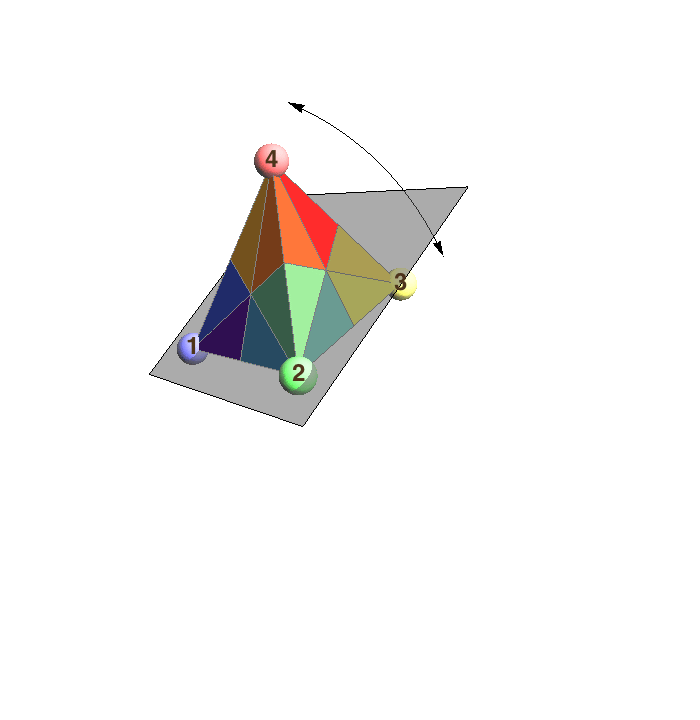
The reflection group of the regular tetrahedron corresponds to the group of permutations of {1,2,3,4}. Shown are three special reflections that interchange 1&2, 2&3, and 3&4.
-
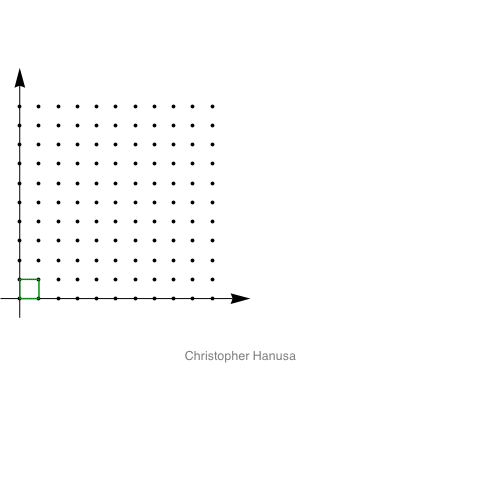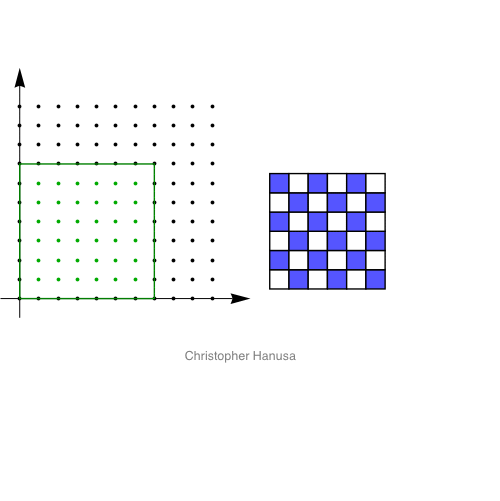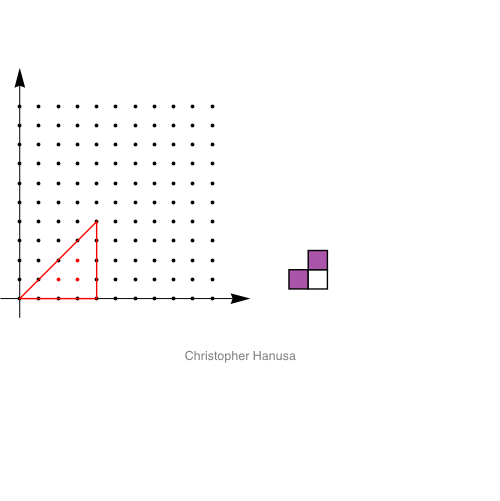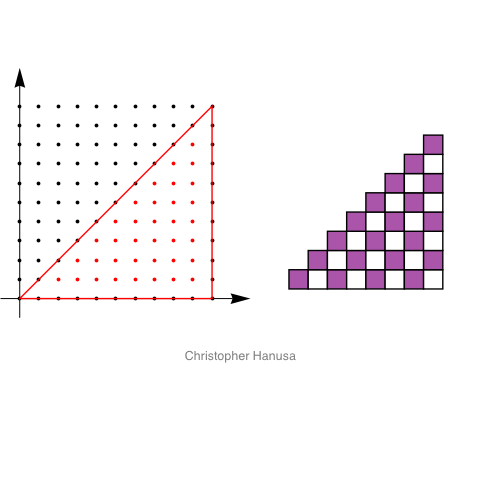
In how many ways can we place q Queens on an nxn chessboard so that no two attack each other? We use Ehrhart theory to answer this question by counting lattice points inside a dilating polygon.
-
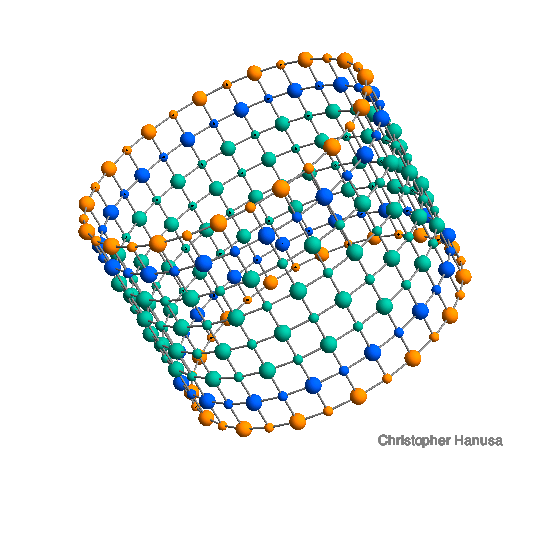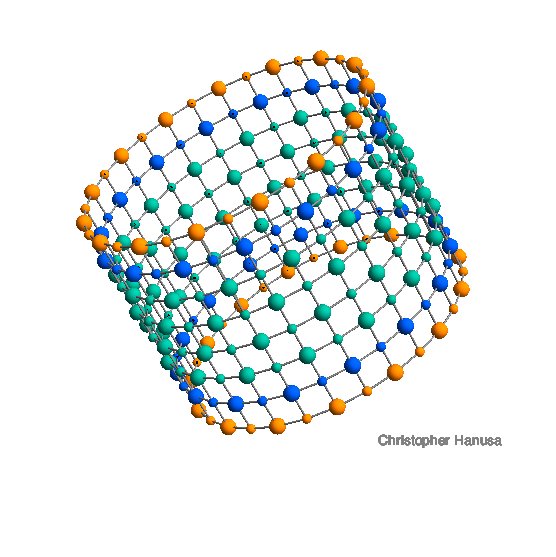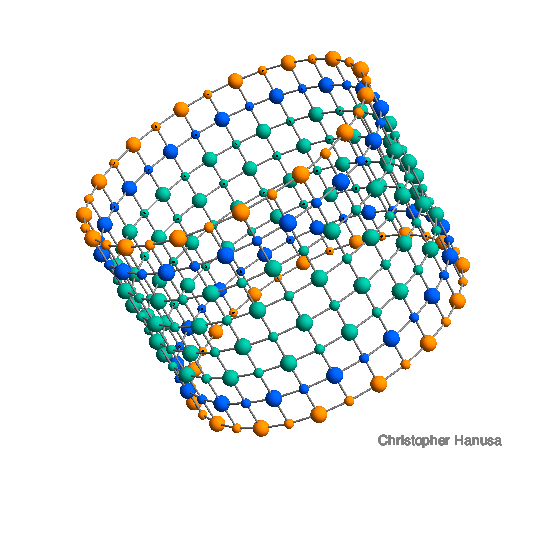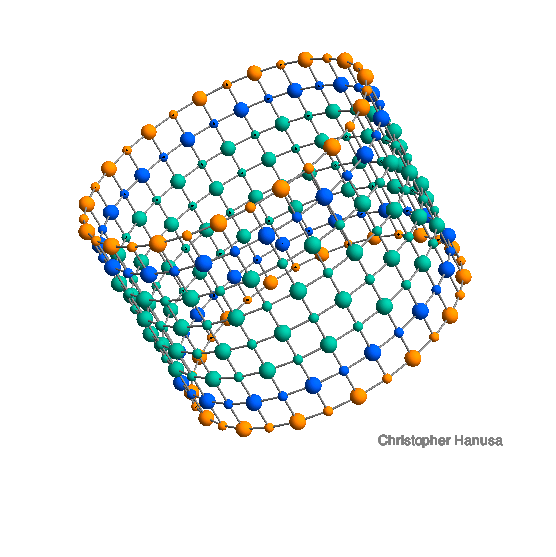
For every ion in a molecule, one can calculate the force it feels from all the other ions in the molecule. This value is the ion's Madelung Constant. Shown is a nanotube with 8 layers of 30 ions.