Back to Final Exams Index



Mathematics 131, Fall 1999, Final Exam




1. The value of a toy is $60. The toy will depreciate constantly to a value of zero over a period of 20 years.

(a) Express the value of the toy after t years.

(b) When will the value of the toy be $30?


2. Find f'(x) for f(x) = 4 - 6x² using only the definition of the derivative




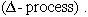
3. Find dy/dx for each of the following. Algebraic simplification is not necessary.





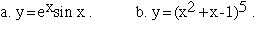
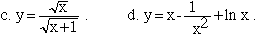
4. A computer manufacturer estimates that if x computers can be produced each month, the total cost will be C(x) = 90000 + 400 x dollars. With a unit proce U(x) = 1600 - 3 x dollars all computers could be sold.

a) Find the revenue function.

b) Estimate, using your graphing calculator, the "break-even" level of production (cost = revenue).

c) Find the profit function.

d) How many computers should be produced to maximize profit?


5. Suppose f(x) = 4x⁴ - 8x² .

(a) Determine when f(x) is increasing, decreasing, concave up, and concave down.

(b) Find all relative extrema and inflection points.

(c) Sketch the graph of y = f(x).


6. A box is to be constructed with a square base and no top. Material for the sides costs $2 per square foot while material for the bottom costs $8 per square foot. If the box costs $2400, find the dimensions which yield the greatest volume.


7. If xy² + 2x² = 3y defines y implicitly as a function of x,

a. find dy/dx at (1,2) and

b. find an aquation of the tangent line to the graph at (1,2).


8. Using the approximation principle, estimate

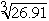without using a calculator.


9. Find the absolute minimum of f(x) = 2x² - 6x + 1 on [ -5/2 , 2 ] .




This material is the property of Queens College and may not be reproduced in whole or in part, for sale or free distribution, without the written consent of Queens College, Flushing, New York 11367.




Back to Final Exams Index