Back to Final Exams Index



Mathematics 141, Fall 1999, Final Exam


1. a) For each of the following limits, find a numerical approximation correct to 5 decimal places using the TABLE menu of your calculator. Reproduce the last 3 entries in each table.





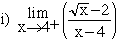
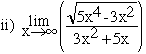
b) Evaluate the limits exactly (without calculator).


2. a) Using the definition of derivative, find f’(x) for



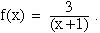
b)



3. Let c be a real number and suppose that


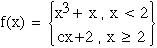
a) Find a value of c which will make f(x) continuous at x = 2 . Explain carefully why the value makes f(x) continuous.

b) Does the value in part (a) also make f(x) differentiable at x = 2? Explain.


4. Find the derivatives. (Do not simplify.)




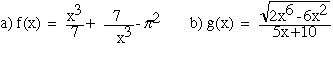
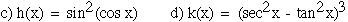
5. Use implicit differentiation to find an equation of the tangent line to the curve xy² - x²y³ + 4y = 2 at the point ( 2 , 1 ) .


6. Sketch a graph of y = f(x) that satisfies










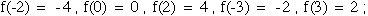
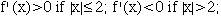
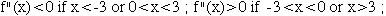
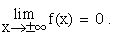
7. a) Approximate to 3 decimal places the absolute maximum and absolute minimum values for f(x) = 3x⁵ - 5x³ + x² + 3 on [ -1.4, 1.4 ].

b) Without using a calculator find the absolute maximum and absolute minimum values of f(x) = 2x³ - 9x² + 12x + 1 on [ 0, 2 ].


8. If tickets to a show are priced at x dollars, where



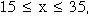
past experience indicates that 800 - 10 x tickets will be sold.

a) What price should be charged in order to maximize the revenue?

b) How many tickets are sold if the revenue is maximized?

9. At 10 AM, a train leaves the station traveling north at 80 mph. At 11 AM, a second train leaves the same station traveling east at 90 mph.

a) How far apart are the trains at 1 PM?

b) At what rate is their distance changing at 1 PM?




This material is the property of Queens College and may not be reproduced in whole or in part, for sale or free distribution, without the written consent of Queens College, Flushing, New York 11367.




Back to Final Exams Index