Back to Final Exams Index



Mathematics 141, Spring 1999, Final Exam


1. Evaluate each of the following limits or explain why it does not exist. If a limit is
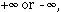state this as your answer.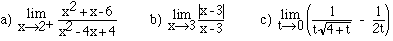




2. Use the Squeeze Theorem to evaluate




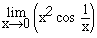
3. Use the TABLE menu of your calculator to find a five decimal place estimate of



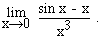
Make a table in your exam book, displaying enough values to justify your answer.


4. Find the derivative of each of the following functions:






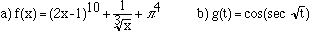
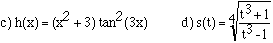
5. Use the definition of the derivative to find f'(x) if f(x) = 1/(3x+1) .


6. Find an equation of the tangent line to the curve xy³ + x³y = 10 at the point (1,2).


7. Sketch a possible graph of a function f that satisfies all of the following conditions:

a) f'(-1) = 0 = f'(2) , f(-1) = -1 = f(2) , f(0) = 0 .

b) f'(x) = 0 for x < -3 , f'(x) < 0 on ( -3 , -1 ) and ( 0 , 2 ) and



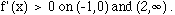
c) f''(x) > 0 on ( -3 , 0 ) and ( 0 , 5 ) and f''(x) < 0 for x > 5 .


8. Find the point on the curve

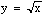that is closest to the point ( 5 , 0 ) .


9. Consider the function

.

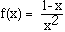a) Use f'(x) to find all intervals where f is increasing or decreasing.

b) Use f''(x) to find all intervals where f is concave up or concave down.

c) Find all points where f has a relative maximum, relative minimum or a point of inflection.

d) Use appropriate limits to find horizontal and vertical asymptotes (if any) for the graph of f(x).

e) Use the information from a) - d) to sketch the graph of

.




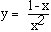This material is the property of Queens College and may not be reproduced in whole or in part, for sale or free distribution, without the written consent of Queens College, Flushing, New York 11367.




Back to Final Exams Index