Back to Final Exams Index



Mathematics 142, Spring 1999, Final Exam


1) Use only the definition of the definite integral (i.e., the limit of the sum of areas of rectangles) to evaluate




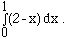
2) Let R be the region bounded by the curves



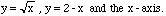
a) Find the area of R.

b) Find the volume of the solid generated by rotating R about the x-axis.

c) Find the volume of the solid generated by rotating R about the y-axis.


3) Consider the region bounded by the curves y = x⁴ - 3x and y = 4x - 2 .

a) Use your calculator to sketch this region and label all points of intersection (to the nearest tenth).

b) Set up the integrals needed to compute the area of this region and the volume of the solid of revolution generated by rotating it about the y-axis.

c) Use your calculator to evaluate the integrals set up in part (b).


4) a) Show that f(x) = 2 tan(x) + x³ + 2 is a one-to-one function in the interval



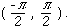
b) Let g be the inverse of f . Find g'(2).


5) Use logarithmic differentiation to find the derivative of




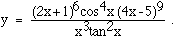
6) Find f'(x) if :






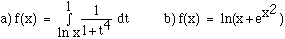
7) Evaluate the following integrals.








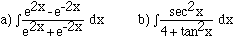
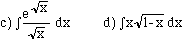
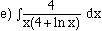
8) A certain population grows at a rate proportional to itself. If in 1980 the population was 10,000 , and in 1990 the population was 16,000 , what was the population in 1985?


9) An object moves in the clockwise direction around the unit circle x² + y² = 1 . As it passes through the point

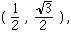
its y-coordinate is decreasing at the rate of 3 units per second. Find the rate of change of its x-coordinate at the same instant.




This material is the property of Queens College and may not be reproduced in whole or in part, for sale or free distribution, without the written consent of Queens College, Flushing, New York 11367.




Back to Final Exams Index