Suppose that a hot object is placed in a surrounding medium of constant temperature (such as a large room). According to Newton, the rate at which the object cools down is proportional to the difference between the temperature of the object and that of the medium. If $T=T(t)$ denotes the temperature of the object at time $t$, and if $S$ denotes the constant temperature of the surrounding medium, then the law translates into the differential equation $$ \frac{dT}{dt} = k (T-S) $$ where $k<0$ is a constant. The solution of this equation, as we have seen, is $$ T=(T_0-S) e^{kt} + S \qquad \qquad (*) $$ where $T_0$ is the initial temperature.
We put this law to a simple test during the lecture on 4/27/17. The temperature of the room was $S=74.6^{\circ}$F. A cup of hot water was left on the table to cool down, and the temperature was recorded every $10$ minutes for one and a half hours, resulting in a total of $10$ samples. The readings were made using an instant digital thermometer:
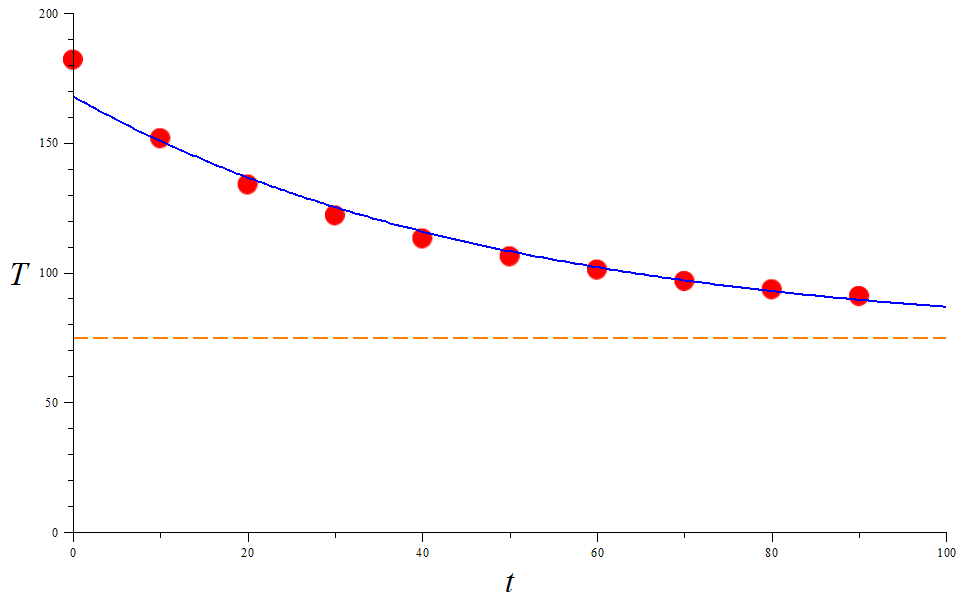
| time $t$ (min) | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 |
| temperature $T$ ($^{\circ}$F) | 182.0 | 151.7 | 133.9 | 122.0 | 113.1 | 106.2 | 101.1 | 96.7 | 93.5 | 90.9 |
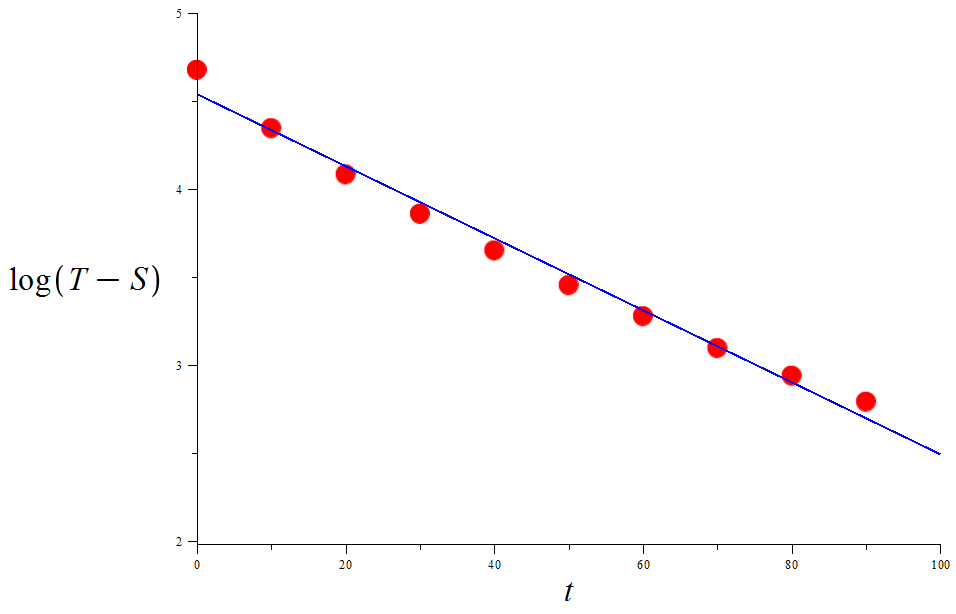
To examine the accuracy of Newton's law, we noted that the exponential model $(*)$ is equivalent to $\log(T-S)$ being linear in time: $$ \log(T-S) = kt+C, \qquad \text{where} \ C=\log(T_0-S). $$ Here are the corresponding $\log (T-S)$ data rounded to 2 decimals, and the resulting plot versus time:
| time $t$ (min) | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 |
| $\log(T-74.6)$ | 4.67 | 4.34 | 4.08 | 3.85 | 3.65 | 3.45 | 3.27 | 3.09 | 2.93 | 2.79 |

|
As seen from this plot, the data nearly follows a linear model. To obtain an empirical value for $k$, we used the standard least-squares method to obtain $$ L(t) = -0.020416 \ t + 4.535718 $$ as the best fitting line (shown in blue), giving $k \approx -0.020416$.
The resulting model $\exp(L(t))+S$ of $T$ along with the sample temperatures are shown below. The horizontal dotted line corresponds to the room temperature $S=74.6$, which is supposed to be $\lim_{t \to +\infty} T(t)$.
|