cross ratios \( \newcommand{\ds}{\displaystyle} \newcommand{\diam}{\operatorname{diam}} \newcommand{\area}{\operatorname{area}} \newcommand{\dist}{\operatorname{dist}} \newcommand{\ord}{\operatorname{ord}} \newcommand{\res}{\operatorname{res}} \newcommand{\wind}{\operatorname{W}} \newcommand{\Aut}{\operatorname{Aut}} \newcommand{\SL}{\operatorname{SL}} \newcommand{\PSL}{\operatorname{PSL}} \newcommand{\iso}{\stackrel{\cong}{\longrightarrow}} \newcommand{\myint}{\operatorname{int}} \newcommand{\ve}{\varepsilon} \newcommand{\es}{\emptyset} \newcommand{\sm}{\smallsetminus} \newcommand{\bd}{\partial} \newcommand{\Chat}{\hat{\mathbb C}} \newcommand{\Cstar}{{\mathbb C}^*} \newcommand{\Rstar}{{\mathbb R}^*} \newcommand{\Dstar}{{\mathbb D}^*} \newcommand{\myre}{\operatorname{Re}} \newcommand{\myim}{\operatorname{Im}} \newcommand{\ov}{\overline} \newcommand{\io}{\iota} \newcommand{\con}{\operatorname{const.}} \newcommand{\OO}{{\mathcal O}} \newcommand{\MM}{{\mathcal M}} \newcommand{\FF}{{\mathcal F}} \newcommand{\CC}{{\mathbb C}} \newcommand{\PP}{{\mathbb P}} \newcommand{\RR}{{\mathbb R}} \newcommand{\HH}{{\mathbb H}} \newcommand{\TT}{{\mathbb T}} \newcommand{\II}{{\mathbb I}} \newcommand{\ZZ}{{\mathbb Z}} \newcommand{\NN}{{\mathbb N}} \newcommand{\DD}{{\mathbb D}} \newcommand{\QQ}{{\mathbb Q}} \newcommand{\SS}{{\mathbb S}} \newcommand{\GL}{\operatorname{GL}} \newcommand{\PGL}{\operatorname{PGL}} \newcommand{\bv}{\boldsymbol{v}} \newcommand{\bu}{\boldsymbol{u}} \newcommand{\bp}{\boldsymbol{p}} \newcommand{\bq}{\boldsymbol{q}} \)




To each ordered quadruple $L_1,L_2,L_3,L_4$ of distinct Euclidean lines in the plane that pass through a given point $p$ one can assign a well-defined real-valued cross ratio $[L_1,L_2,L_3,L_4]$. To see this, take an arbitrary line $L$ not containing $p$, look at the intersection points $\{ z_i \} := L \cap L_i$ (we set $z_i:=\infty$ if $L$ is parallel to $L_i$), and set
Figure 1
\[ [L_1,L_2,L_3,L_4] := [z_1,z_2,z_3,z_4] = \frac{(z_3-z_1)(z_4-z_2)}{(z_2-z_1)(z_4-z_3)}. \] Of course one needs to check that this definition is independent of the choice of the line $L$. In other words, if $L'$ is another line not containing $p$ and $\{ w_i \} := L' \cap L_i$, then \[ [z_1,z_2,z_3,z_4] = [w_1,w_2,w_3,w_4] \qquad \qquad (\dagger) \] (see Fig. 1). This claim appears as problem 7 in Chapter 4 and can be proved in several ways. One idea (as the “hint” suggests) is to observe that $[z_1,z_2,z_3,z_4]$ can be expressed solely in terms of sines of the angles between the $L_i$ at $p$ and therefore must equal $[w_1,w_2,w_3,w_4]$. In fact, if $\alpha, \beta, \gamma$ denote the angles between the pairs $(L_1,L_2), (L_2,L_3), (L_3,L_4)$ respectively, then an easy geometry exercise shows that \[ [z_1,z_2,z_3,z_4]= \frac{\sin(\alpha+\beta) \ \sin(\beta+\gamma)}{\sin \alpha \ \sin \gamma}. \]
Figure 2

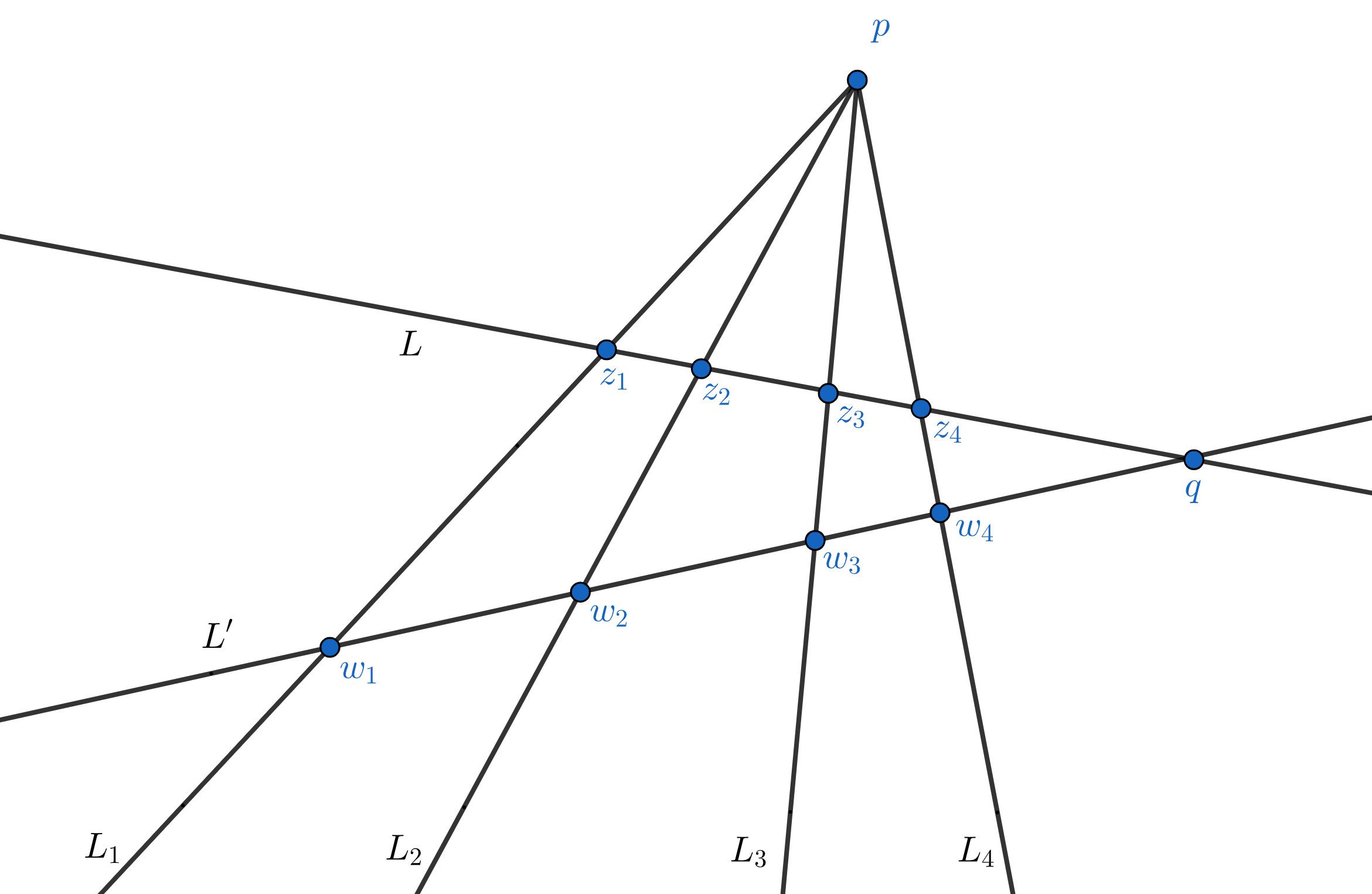
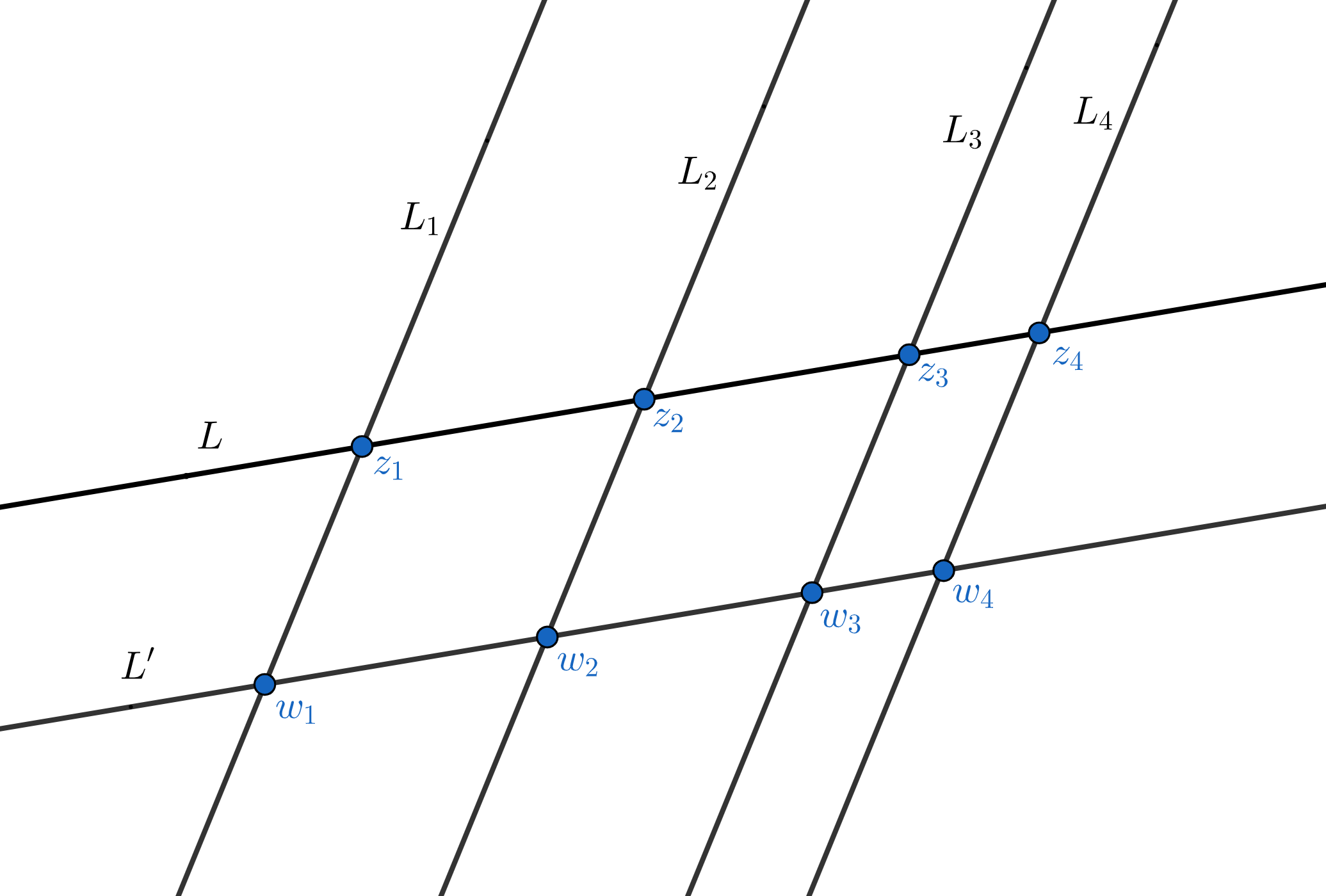
A more intrinsic approach is to take advantage of the real projective geometry of the plane (for an excellent introduction to projective spaces, see I. Shafarevich and A. Remizov, Linear Algebra and Geometry, Springer, 2013). Very briefly, the idea is to compactify $\RR^2$ by adding a projective line (=circle of directions) at infinity to obtain what is known as the real projective plane $\RR\PP^2$. Each line in the plane intersects the line at infinity at a single point, so its closure in $\RR\PP^2$ is a topological circle. The automorphism group of $\RR\PP^2$ is the group $\PGL_3(\RR)$ of real projective transformations isomorphic to the matrix group $\GL_3(\RR)$ modulo the subgroup of all non-zero multiples of the identity matrix. $\PGL_3(\RR)$ acts transitively on lines, on triples of colinear points, and on quadruples of points in general position (i.e., when no three of the four points are colinear). Moreover, elements of $\PGL_3(\RR)$ preserve cross ratios of colinear quadruples. Using real projective transformations the proof of $(\dagger)$ becomes trivial: Let $q$ be the intersection point of $L,L'$ and take a projective transformation which maps the line through $p,q$ to the line at infinity in $\RR\PP^2$. Under this transformation the lines $L,L'$ and the lines $L_1,L_2,L_3,L_4$ are mapped to parallel lines (see Fig. 2) for which the equality of the cross ratios is immediate.

It is interesting that the same result can be deduced using the complex projective geometry of the plane, i.e., by invoking Mobius transformations (at first glance this idea may seem a bit ill-suited since Mobius maps do not preserve straight lines). Going back to Fig. 1, consider the perspective map $L \to L'$ which sends each $z \in L$ to the point $w$ where the line through $p,z$ meets $L'$ (the point $p$ is often called the vanishing point of this perspective map). The equality in $(\dagger)$ will be an immediate corollary of the following

Lemma 1. The perspective map $L \to L'$ extends to a Mobius transformation.

Notice that the result holds for any vanishing point $p$ outside the union $L \cup L'$.

Proof. After a complex affine change of coordinates (which preserves lines) we may assume $L'=\RR$ and $p=i$. The line $L$ has an equation of the form $\lambda z + \ov{z} + \mu=0$ for some $\lambda, \mu \in \CC$ with $|\lambda|=1$. For each $z \in L$ the colinearity of $i,z,w$ implies \[ \frac{z-i}{\ov{z}+i} = \frac{w-i}{\ov{w}+i} = \frac{w-i}{w+i}. \] Solving for $w$ and using $\ov{z}=-\lambda z -\mu$ we obtain \[ w = i \, \frac{(\lambda-1)z+\mu}{(\lambda+1)z+\mu-2i}. \] This is the restriction of a Mobius transformation. In fact, \[ \det \begin{bmatrix} \lambda-1 & \mu \\ \lambda+1 & \mu-2i \end{bmatrix} = -2(\lambda i - i + \mu), \] which is non-zero since $p=i$ is not on the line $L$. $\Box$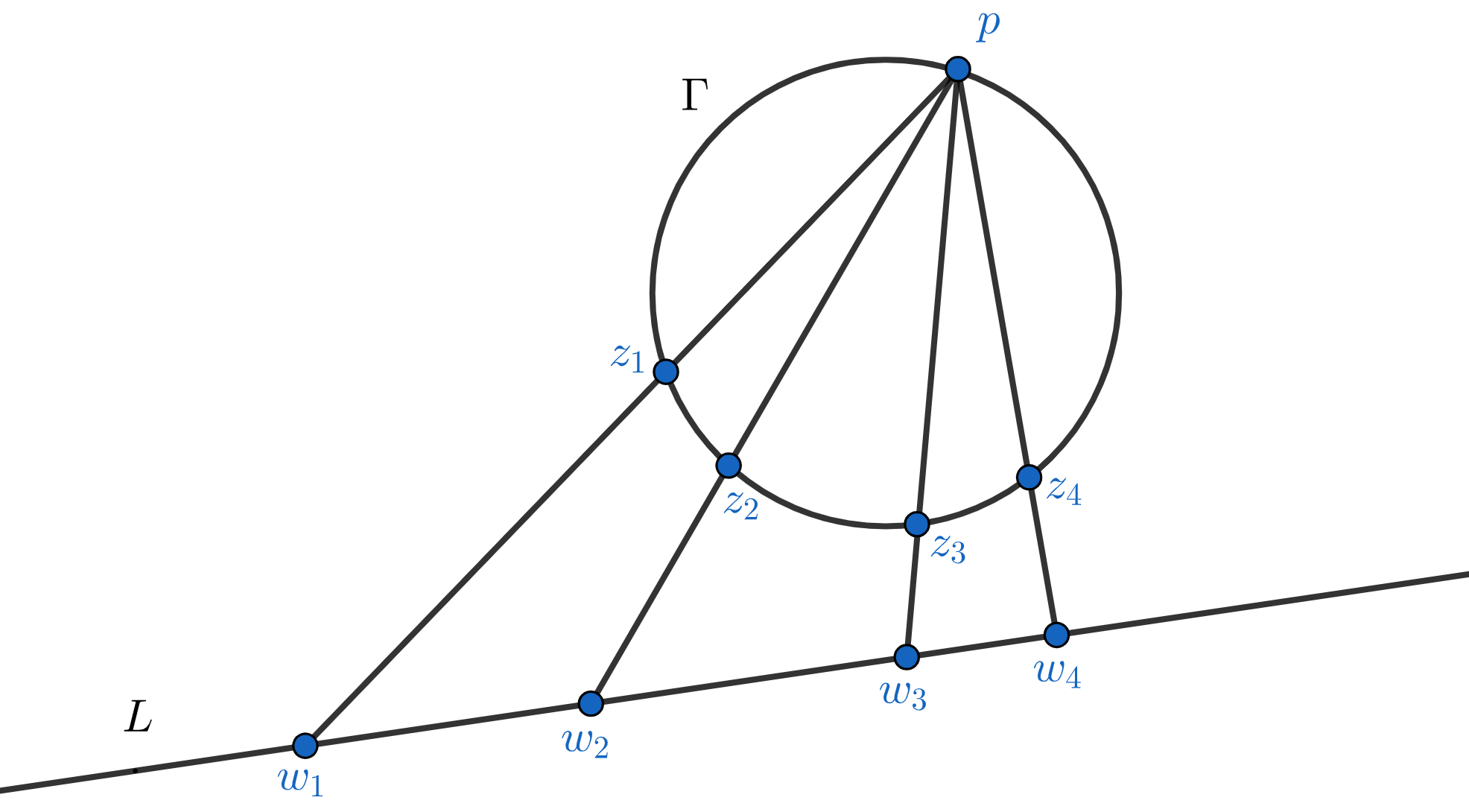
Figure 3

The cross ratio $[L_1,L_2,L_3,L_4]$ can be defined using circles passing through $p$ instead of lines avoiding $p$. In other words, if $\Gamma$ is a circle (or in fact any conic section) passing through $p$, and if $\{ z_i \} := \Gamma \cap L_i$, then \[ [L_1,L_2,L_3,L_4] = [z_1,z_2,z_3,z_4]. \] By Lemma 1 it suffices to show that if $L$ is any line not containing $p$ and $\{ w_i \} := L \cap L_i$, then \[ [z_1,z_2,z_3,z_4] = [w_1,w_2,w_3,w_4] \] (see Fig. 3). To see this, consider the one-dimensional stereographic projection $\Gamma \to L$ which sends each $z \in \Gamma$ to the point $w$ where the line through $p,z$ meets $L$. The above cross ratio invariance will follow immediately from the following

Lemma 2. The stereographic projection $\Gamma \to L$ extends to a Mobius transformation.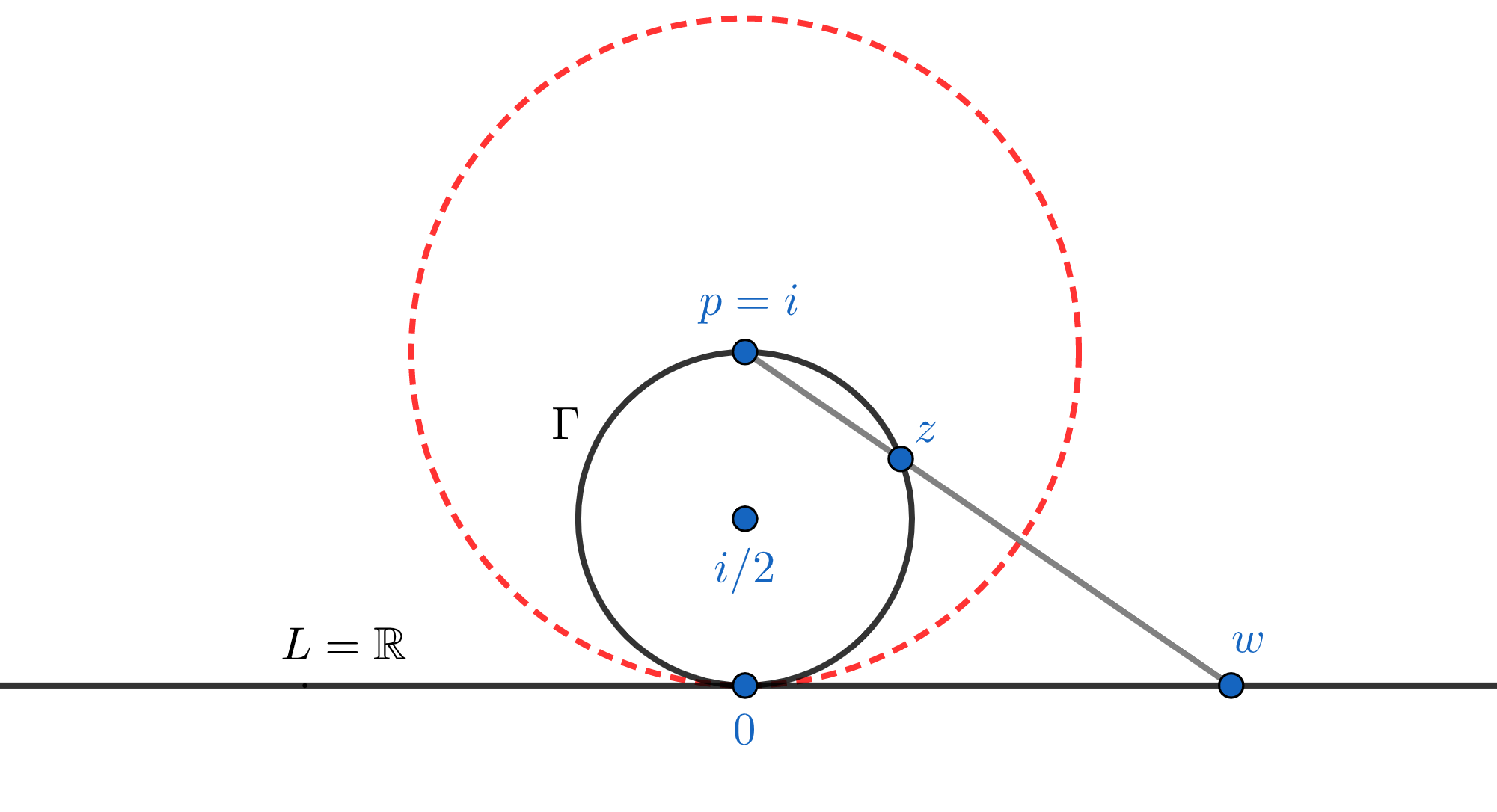

Figure 4

Notice that unlike the situation of Lemma 1, the projection point $p$ must now be restricted to the circle $\Gamma$.

Proof. After a complex affine change of coordinates (which preserves lines and circles) we may assume $p=i$ and $\Gamma$ is the circle $|z-i/2|=1/2$ (see Fig. 4). Moreover, by Lemma 1 it suffices to consider the case where $L=\RR$ because for a general $L$ the stereographic projection $\Gamma \to L$ is the composition of the stereographic projection $\Gamma \to \RR$ followed by the perspective map $\RR \to L$. But these normalizations render the lemma almost trivial: Since reflection in the circle $|z-i|=1$ given by the formula $z \mapsto 1/(\ov{z}+i) +i$ restricts to the projection $\Gamma \to \RR$, its complex conjugate \[ w = \frac{1}{z-i} -i \] would be a Mobius extension of the stereographic projection $\Gamma \to \RR$. $\Box$

Here is an application of the cross ratio of four concurrent lines in a classical theorem of plane geometry: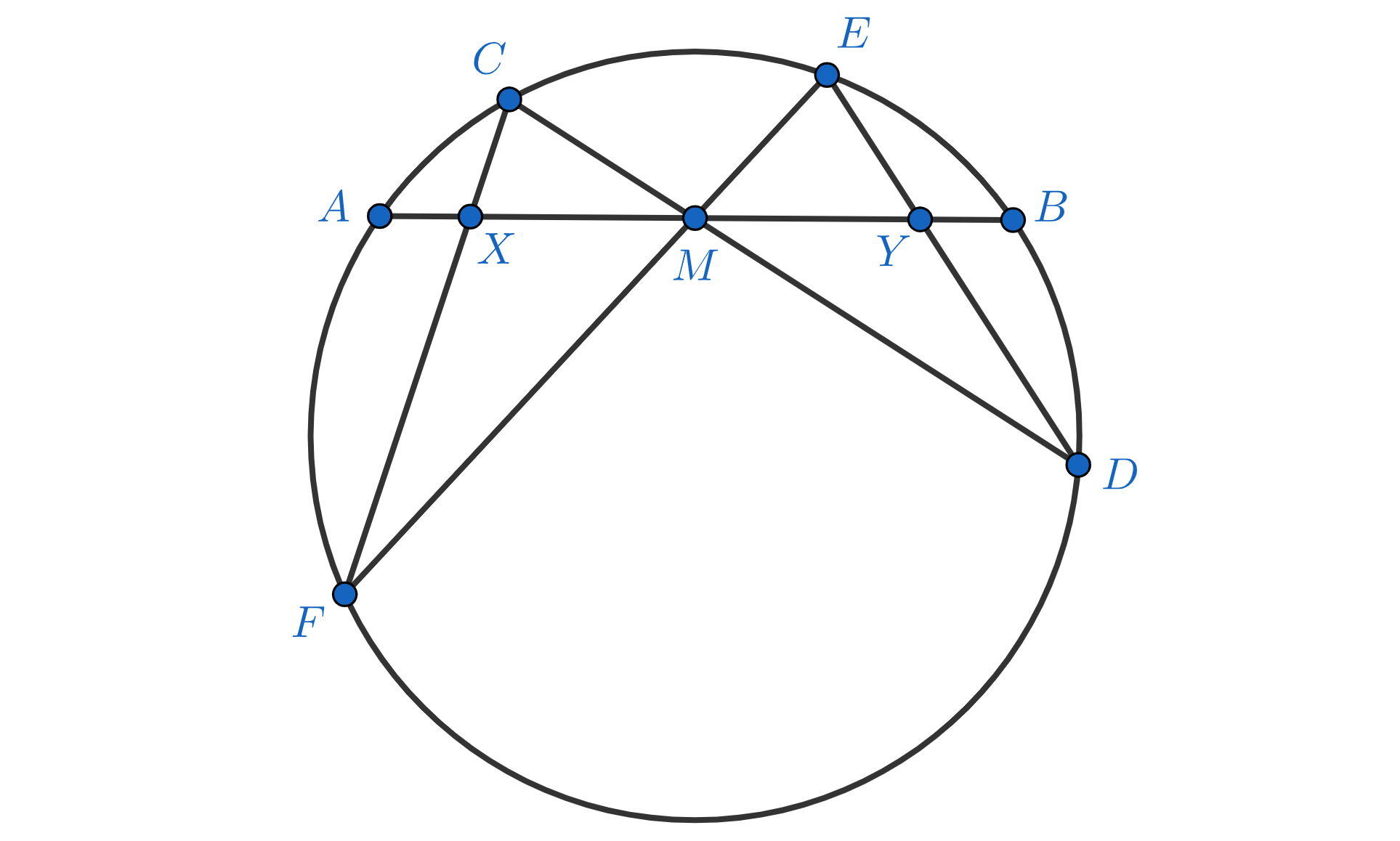

Figure 5

Butterfly Theorem. Suppose $AB$ is a chord of a circle having $M$ as its midpoint. Draw two arbitrary chords $CD$ and $EF$ through $M$ and let $X,Y$ be the intersection points of the lines $CF, DE$ with $AB$. Then $M$ is also the midpoint of $XY$ (see Fig. 5).

Proof. Let $\Gamma$ be the circle in question and $L$ be the line passing through $A,B$. By Lemma 2 applied to the stereographic projection $\Gamma \to L$ from $C$, \[ [A,F,D,B] = [A,X,M,B]. \] Similarly, by Lemma 2 applied to the stereographic projection $\Gamma \to L$ from $E$, \[ [A,F,D,B] = [A,M,Y,B]. \] Calling $a:=|AM|=|MB|$, $x:=|XM|$, $y:=|MY|$, this shows \[ \frac{a \cdot (a+x)}{(a-x) \cdot a} = [A,X,M,B] = [A,M,Y,B] = \frac{(a+y) \cdot a}{a \cdot (a-y)}, \] or $(a-x)(a+y)=(a+x)(a-y)$, which yields $x=y$. $\Box$

Back to notes and comments