I've posted the notes and topics for each day and what is expected of you in and out of class. This schedule is approximate and subject to change! Check back here often.
Monday, January 31
- Notes from Section 1.1 (Notes pages 0–19) '
- What is combinatorics?
- Syllabus discussion.
- Meet your classmates
- Simple Counting
- Multiplication Principle
Wednesday, February 2
Before Class:
- Visit and explore our Microsoft Teams Group
- Visit our Microsoft Teams group. Remember to log in with username FirstName.LastName##@login.cuny.edu instead of FirstName.LastName##@qmail.cuny.edu.
- Go to the Introductions channel. Introduce yourself to your classmates and share a fun link or meme. Please feel free to reply to a fellow classmate's post if something they share speaks to you.
- Go to the Chat section of Microsoft Teams on the far left menu. (Note: This is a feature outside our Classroom Team.) Send me (Christopher Hanusa) a quick note where you say "Hello Prof. Hanusa", includes the class you are in (MATH 636) and the name you prefer to be called. Feel free to include your preferred pronouns. Think of this as opening a dialog with me that we can continue throughout the semester when you need to get in contact with me.
- Thoroughly read all pages of the course webpage. This should answer all the questions that you may have about the class. Make sure you read carefully about how standards-based grading works.
- Fill out this Doodle to let me know when you are available for office hours this semester. (Pretend like it is a normal week with no holidays --- select the times when you would be able to come to office hours regularly.) I will try to choose times that work for most people.
- (Download / Print out) the notes for class (links below)
- Background reading: Combinatorics: A Guided Tour, Sections 1.1
- Prepare to answer the following thought questions in class.
- Question 1. Answer Exercise 1.1.2ab (This means parts (a) and (b) in Problem 2 of Section 1.1). Then: (c) Assuming the coin is fair, what is the probability that a sequence of 20 flips has exactly 10 heads and 10 tails (in any order)?
- Question 2. How many orderings are there for a deck of 52 cards if all the cards of the same suit are together?
In class:
- Homework Discussion
- Multisets
- Notes from Sections 1.2 & 2.2 (Notes pages 20–26) '
- Counting pitfalls
Monday, February 7
Before Class:
- Schedule some time before Wednesday February 9 to meet for one hour outside of class with at least one other classmate. Your goal is to get together to talk about combinatorics, working together to answer the thought questions.
- Background reading: Combinatorics: A Guided Tour, Sections 1.1 and 1.2
- Prepare to answer the following thought questions in class.
- Question 3. (a) How many subsets of [30] contain no prime numbers? (b) How many subsets of [30] have size 15 and no numbers larger than 20? (c) How many multisubsets of [30] of size 13 have smallest element 6 and largest element 17?
- Question 4. Answer Exercise 1.2.2.
In class:
- Homework Discussion
- Notes from Section 1.3 (Notes pages 27–35) '
Wednesday, February 9
Before Class:
- Background reading: Combinatorics: A Guided Tour, Sections 1.1 and 1.2
- Prepare to answer the following thought questions in class.
- Question 5. Answer Exercise 1.2.13.
- Question 6. (a) Answer Question 1.1.5. Then: (b) Among all ways to choose fifteen coins, what is the smallest amount of money that occurs in at least two different ways? (For example, 15 dimes equals $1.50.)
In class:
- Continuation of previous set of notes.
- Overcounting, Counting the complement
Monday, February 14
Before Class:
- Background reading: Combinatorics: A Guided Tour, Section 1.3
- Prepare to answer the following thought questions in class.
- Question 7. In chess, a rook is a piece that can move only vertically and horizontally. Therefore, two rooks attack each other if they are placed in the same row or in the same column. A non-attacking configuration of rooks consists of placing some number of rooks on a chessboard so that no pair of rooks attack each other. Determine the number of non-attacking configurations of five indistinguishable rooks on an 8x8 chessboard.
- Question 8. 1.2.11
- Question 9. Answer each of the following SIX jeopardy questions by giving a "real world" situation that could be counted by the given quantity. Exercises 1.2.1abcd, 2.1.1c, 2.2.1a
In class:
- Continuation of previous set of notes.
- Bijections
Bijection Worksheet
Wednesday, February 16
Before Class:
- Prepare for Assessment 1 on Standards 1–2.
In class:
- Bijections
- Assessment 1 on Standards 1–2.
No class Monday, February 21.
Wednesday, February 23
Before Class:
- Prepare to answer the following thought questions in class.
- Question 10. Suppose k≤n.
- How many functions are there from [k] to [n]?
- How many bijections are there from [k] to [n]?
- How many one-to-one functions are there from [k] to [n]?
- How many onto functions from [k] to [n] are not one-to-one?
- Come up with the bijection between k-subsets of [n] and n–k-subsets of [n].
- Complete parts (a) and (b) of the Bijection Worksheet.
- Background reading: Combinatorics: A Guided Tour, Section 1.4
In class:
- Bijection Worksheet
- Pascal's triangle and the binomial theorem
Monday, February 28
Before Class:
- Prepare to share your thoughts about the exploration discussed here.
- Exploration Question: Let an be the maximal number of pieces into which you can cut a circle using n lines. Determine by hand the first few values of an. Use the Online Encyclopedia of Integer Sequences to determine what the formula is for an as a function of n.
Once you have found the sequence, there are links right after the first few terms of the sequence. You should look at the graph of the sequence and listen to the sequence. Write down the 42nd term of the sequence.
Then, via the WebCam link at the bottom of the page, look through a few sequences and write down a sequence that looks interesting (its sequence number, its description, and a few first terms) and write a paragraph or two about why you thought it was interesting. We'll share that with our classmates in class. - Prepare to answer the following thought questions in class.
- Question 10 from above.
- Question 11. Create and prove a bijection between two-member subsets of {1, 2,..., n, n+1} and all possibilities of placing one pair of parentheses in a string of n letters. For example, when n=3, we see that there are six two-member subsets of {1,2,3,4}:
{1,2}, {1,3}, {1,4}, {2,3}, {2,4}, and {3,4}.
and there are six ways to place one pair of parentheses in the word abc:(a)bc, a(b)c, ab(c), (ab)c, a(bc), and (abc).
Notice that "a()bc" is not valid—there are no letters between the parentheses. - Question 12. Exercise 2.2.8
- Background reading: Combinatorics: A Guided Tour, Section 1.4
In class:
- Notes from Section 1.4 (Notes pages 36–42) '
- Homework Discussion
- Equivalence classes
- Counting using symmetry
Wednesday, March 2
Before Class:
- Prepare for Assessment 2 on Standards 3–4.
In class:
- Equivalence classes
- Counting using symmetry
- Assessment 2 on Standards 3–4.
Monday, March 7
Before Class:
- Prepare to answer the following questions in class.
- Question 13.
(a) Exercise 1.4.15
(b) Write a paragraph explaining why we can not use the equivalence principle to count the number of different necklaces where two of the n beads are indistinguishable (the same color, for example). - Question 14. Exercise 1.4.13.
- Question 13.
(a) Exercise 1.4.15
- Background reading: Combinatorics: A Guided Tour, Sections 2.1, 2.2, and 4.2
In class:
- Homework Discussion
- Notes from Sections 2.1, 2.2, and 4.2 (Notes pages 43–51) '
- Combinatorial proofs
Wednesday, March 9
Before Class:
- Prepare to answer the following questions in class.
- Question 15. Understand and explain to the class the proof of Theorem 2.1.2. The proof relies on the argument given in Combinatorial Proof #2 on page 55 and the solution to Question 62.
- Question 16. Give a combinatorial proof of the identity in Exercise 2.2.4f.
In class:
- Tiling interpretation of Fibonacci numbers
- Worksheet on Combinatorial proofs
Monday, March 14 (Pi Day!)
Before Class:
- Read the details about our course project.
- Prepare to answer the following question in class.
- Question 17. Use the square-domino interpretation of the Fibonacci numbers to give a combinatorial proof that f2n=1+Σ1≤i≤n f2i-1.
- The assessment for Standards 5 and 6 will be in class on Wednesday.
In class:
- Homework Discussion
- Notes from Sections 2.1 through 2.4 (Notes pages 52–61) '
- Counting distributions
- The sixteenfold way
- Set partitions and the Stirling numbers
Wednesday, March 16
Before Class:
- Prepare to answer the following questions in class.
- Question 18. Exercise 2.1.6
- Question 19. Figure out the answer to each of the following parts. Prove at least one of them using a bijection.
- How many set partitions of [n] into two blocks are there? (Definition of block on p. 35)
- How many set partitions of [n] into (n-1) blocks are there?
- How many set partitions of [n] into (n-2) blocks are there?
- Prepare for Assessment 3 on Standards 5 and 6.
In class:
- Homework Discussion
- Integer Partitions
- Assessment 3 on Standards 5 and 6.
Monday, March 21
Before Class:
- Brainstorm some topics that would be exciting to explore for your project. You do not need to know how to count them yet, but I'd like you to narrow down your topic to one or two ideas.
- Project topic due today. Send Prof. Hanusa an email before class with the precise question you plan to answer.
- Prepare to answer the following questions in class.
- Question 20. Exercise 2.3.4
- Question 21. Exercise 2.4.1
- Background reading: Combinatorics: A Guided Tour, Section 3.1
In class:
- Discussion of homework questions.
- Notes from Section 3.1 and pp. 165–166 (Notes pages 62–68) '
- Principle of Inclusion/Exclusion
- Derangements
Wednesday, March 23
Before Class:
- Revise your project topic if necessary before class. Make sure you have a precise problem statement so you can spend time thinking about your project next week.
- Prepare to answer the following questions in class.
- Question 22. Exercise 3.1.4(a) Hint: Define A1 to be the set of 13-card hands that have no spades. (Or call it A♠!)
- Question 23. Exercise 3.1.17
In class:
- Homework Discussion
- Notes from Sections 3.3 and 3.4 (Notes pages 69–77) '
- Introduction to generating functions
- Application: Fruit baskets
- Coefficient Extraction
Professor Hanusa will be out of town at a research workshop this week. Monday will be in person but Wednesday will be asynchronous. See below.
Monday, March 28
Before Class:
- Prepare for Assessment 4 on Standards 7 and 8.
In Class:
- Assessment 4 on Standards 7 and 8.
- The remainder of class can be used to take reassessments on standards of your choice.
Wednesday, March 30
Outside Class:
- There will be no formal class today. Instead, spend time outside class working on your project. Your goal should be to develop some combinatorial understanding of your question with a plan about how to use combinatorial techniques to answer your question. This will probably involve writing out some specific cases to get a feel for the problem and what answers to the problem look like.
- I will post a video lecture that completes the notes from class last week on generating functions.
Monday, April 4
Before Class:
- Prepare to answer the following questions in class. I suggest meeting outside of class with your classmates to work on them. Feel free to use Wolfram Alpha or Mathematica to look at the coefficients of this generating function. Recall that the Mathematica command to find the coefficients of the generating function from class is:
Series[1/(1-x)/(1-x^2)/(1-x^3),{x,0,98}]
- Question 24. Exercise 3.3.2(a,b,c,d,e,f) on page 113.
- Question 25. Exercise 3.3.3(a,c,d). First give an answer involving binomial coefficients and multinomial coefficients by hand, then use Wolfram Alpha or Mathematica to verify your work. Try parts (b) and (e) for a challenge.
- Question 26. Exercise 3.3.7. First create the generating function. (It won't have a nice compact form.). Then use Wolfram Alpha or Mathematica to solve the question.
In class:
- Homework Discussion
- Notes from external material (Notes pages 78–88) '
- Products of generating functions and their interpretation
- Application: Dice
- Vandermonde's Identity
- Powers of generating functions and their interpretation
Wednesday, April 6
Before Class:
- Prepare to answer the following questions in class. Feel free to use Wolfram Alpha or Mathematica.
- Question 27.

- Question 28. Suppose you roll three six-sided dice. Calculate the probability that the dice sum to fourteen. Now suppose you roll five six-sided dice. Calculate the probability the dice sum to fourteen. Which probability is higher?
- Question 29. Give a combinatorial counting question whose answer is the coefficient of xk in the generating function (1+x)10/(1-2x)
In class:
- Homework Discussion
- Compositions
- Compositions of generating functions and their interpretation
Monday, April 11
Before Class:
- Spend some time thinking about your project. Bring what you have so far to class.
- Prepare to answer the following questions in class.
- Question 30.
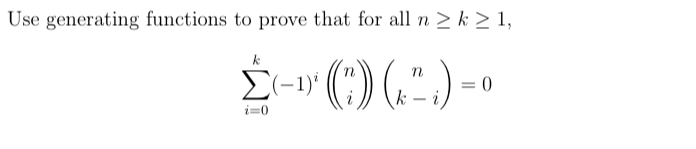
- Question 30.
In class:
- Homework Discussion
- Compositions of generating functions and their interpretation
- Prof. Hanusa will come around and discuss your project progress and make sure you can make some progress over the next few weeks.
Wednesday, April 13
Before Class:
- You may want to think about Questions 31 and 32 while the material is still fresh in your mind.
- Prepare for Assessment 5 on Standards 9 and 10.
In class:
- Notes from Sections 2.4, 3.4, and 4.4 (Notes pages 89–96) '
- Integer partitions
- Standard Young Tableaux
- Assessment 5 on Standards 9 and 10.
Monday, April 25
Before Class:
- Prepare to answer the following questions in class.
- Question 31. Calculate the generating function that counts how many ways are there to take a line of n soldiers, break them into non-empty platoons, and choose some (possibly empty) subset of each platoon to be on "night watch". (Consider compositions of generating functions.) For an extra challenge, calculate this number as a function of n.
- Question 32. Suppose you have an unlimited supply of black building blocks of height 1 and an unlimited supply of red, orange, yellow, green, blue, and purple building blocks of height 2. Calculate the generating function that counts the number of ways to build a tower of height n? (Consider compositions of generating functions.) For an extra challenge, calculate the exact number as a function of n.
- Question 33. (a) Determine the generating function for the number of partitions of n such that there are at most two parts of the same size. [For example, 511 is OK, but 4111 is not allowed since 1 appears thrice.] (b) Determine the generating function for the number of partitions of n such that the parts are all of size equal to a power of two. [For example: 84422 is OK, but 744221 is not because 7 is not a power of two.]
- Question 34. Enumerate the Standard Young Tableaux of shape 3+3. Ensure that the number of SYT that you enumerated agrees with the formula from the notes. For an extra challenge, enumerate the SYT of shape 4+4.
In class:
- Homework Discussion
- Notes from Section 4.1 PLUS additional material (Notes pages 97–105) '-->
- Catalan numbers
- Catalan number interpretations
- Catalan bijections
- (Handy handout about Catalan numbers)
- (link to Stanley's Catalan Interpretations)
Wednesday, April 27
Before Class:
- Prepare to answer the following questions in class.
- Question 35. Find and list the appropriate 14 triangulations, Dyck paths, +1/-1 sequences, and multiplication schemes that are counted by the Catalan numbers.
- Question 36. Given the 14 triangulations and 14 Dyck paths you calculated in Question 35, use the bijections from class to determine which Dyck path corresponds to which triangulation.
- Prepare for Assessment 6 on Standards 11 and 12.
In class:
- The "meta" method for Catalan numbers
- A formula for the Catalan numbers
- Assessment 6 on Standards 11 and 12.
Monday, May 2
Before Class:
- Prepare to answer the following questions in class.
- Question 35. Use a bijection to show that sequences
1≤ a1≤ a2≤ … ≤ an of length n, where each ai≤ i are also counted by the Catalan number Cn. For example, when n=3, the five sequences are 111, 112, 113, 122, and 123. [Hint: Look at the boxes to the left of a Dyck path.] - Question 36. Another family of combinatorial objects that is counted by the Catalan numbers are rooted plane trees. (See Section 1.6 of the Handy handout about Catalan numbers.) Combinatorially show that these objects satisfy the generating function equation C(x)=1+xC(x)2. (This will be a "meta" argument similar to the ones from class.)
- Question 35. Use a bijection to show that sequences
- Think to schedule some office hours if you are having difficulty with your project.
In class:
- Homework Discussion
- Notes on Combinatorial Statistics (Notes pages 106–116) '
- Combinatorial statistics
- Descent statistic des(π)
- Inversion statistic inv(π)
- Major statistic maj(π)
- q-analogs
- q-factorial
- q-binomial coefficients
- PDF about q-analogs
Wednesday, May 4
Before Class:
- Prepare to answer the following questions in class.
- Question 37.
- Calculate des(π), inv(π), and maj(π) for π=963852741.
- Let π be an n-permutation with reverse σ. How is inv(π) related to inv(σ)?
- Question 38. Two combinatorial interpretations of the q-binomial coefficients are given on page 120 of the course notes.
- Show that for permutations π of the multiset {1,1,2,2,2},
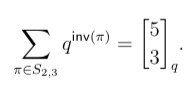
- Show that for the set of lattice paths P from (0,0) to (2,3)$,
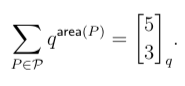
- Show that for permutations π of the multiset {1,1,2,2,2},
- Question 39.

- Question 37.
- Prepare for Assessment 7 on Standards 13 and 14.
In class:
- Homework discussion
- Catch-up with topics
- Assessment 7 on Standards 13 and 14.
Monday, May 9
Before Class:
- Spend some time thinking about your project. Bring what you have so far to class.
In class:
- Homework discussion or Current research in combinatorics
- In-class time for Poster Work
Wednesday, May 11
Before Class:
- Prepare for Assessment 8 on Standards 15 and 16.
In class:
- Assessment 8 on Standards 15 and 16.
- Remainder of class: Reassessments or Poster Work Day
Monday, May 16
Before Class:
- Continue work on Poster. Bring what you have to class so far.
In class:
- In-class project work day and Peer review
Wednesday, May 18, 1:45-3:45pm
Before Class:
- Complete work on your poster.
- Bring it to class at 1:45pm.
In class:
- Poster Session