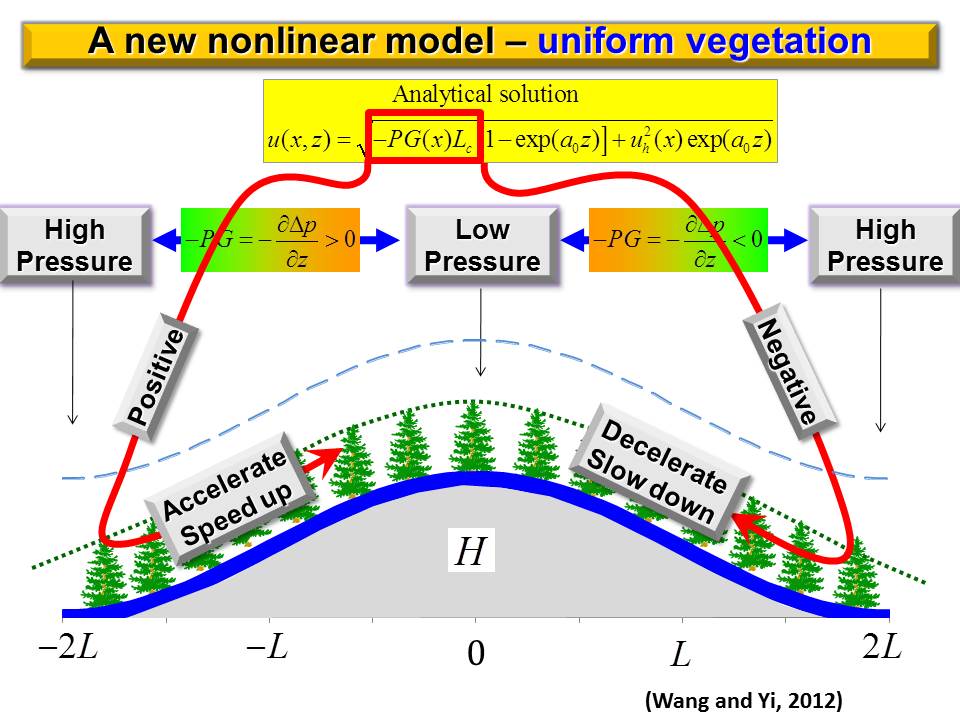
The real world surface is not flat and most is covered by vegetation. A forested hill can be viewed as a conceptual unit to understand essentials in complexity created by different hill geometry and plant morphology in the real world. Analytical research into flows within and above vegetation of a forested hill has many implications, including improvements of the land surface parameterization of numerical weather prediction models, and theoretical understanding of mechanisms behind the advection problems in eddy-flux measurements.

 

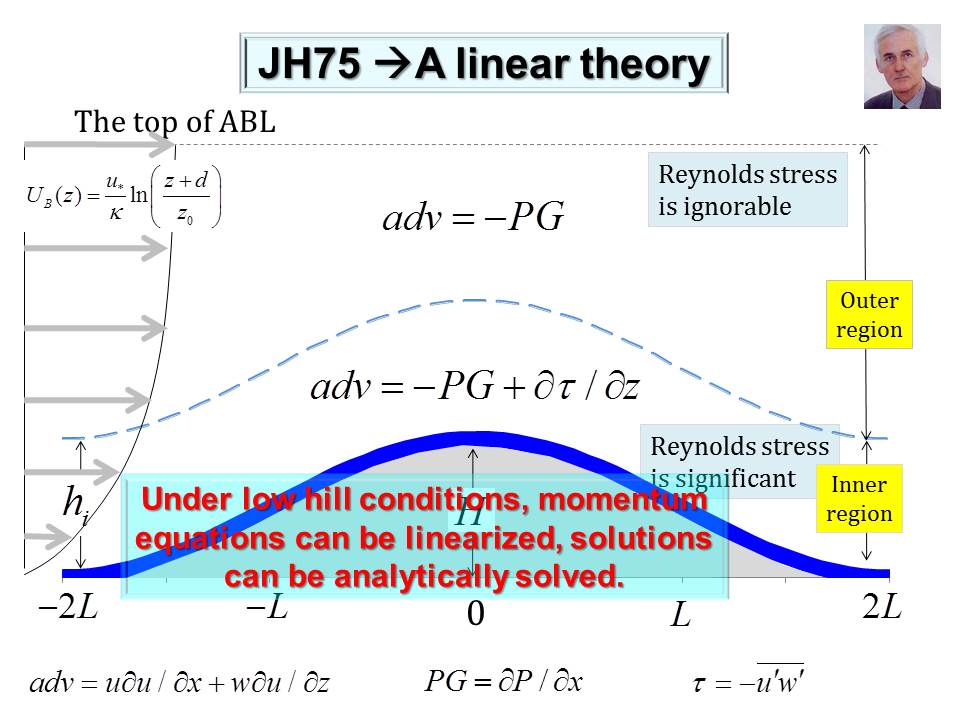
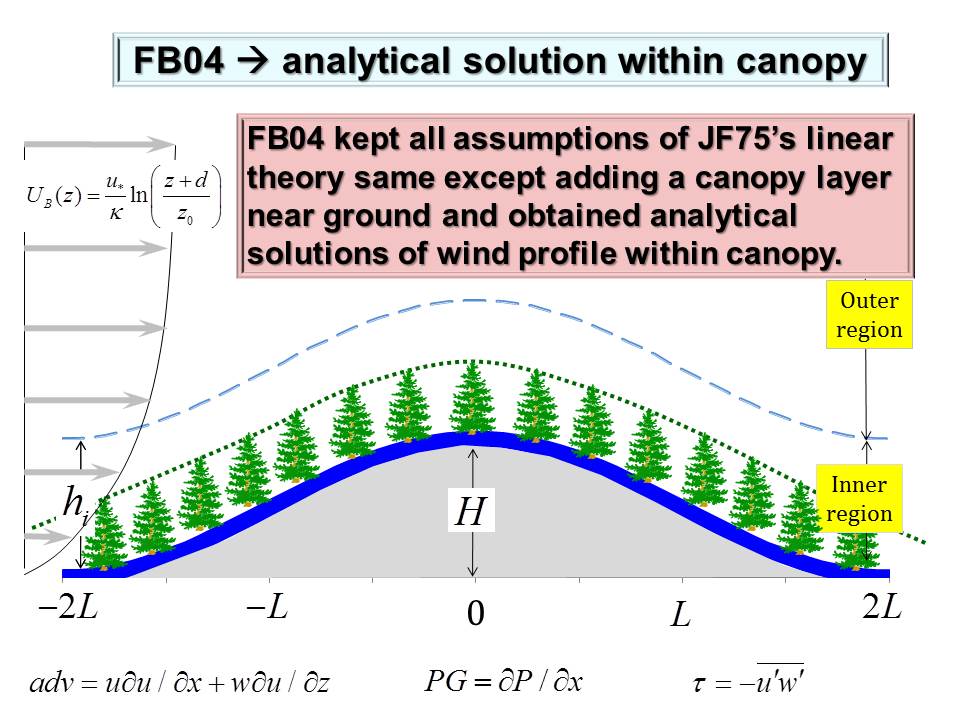
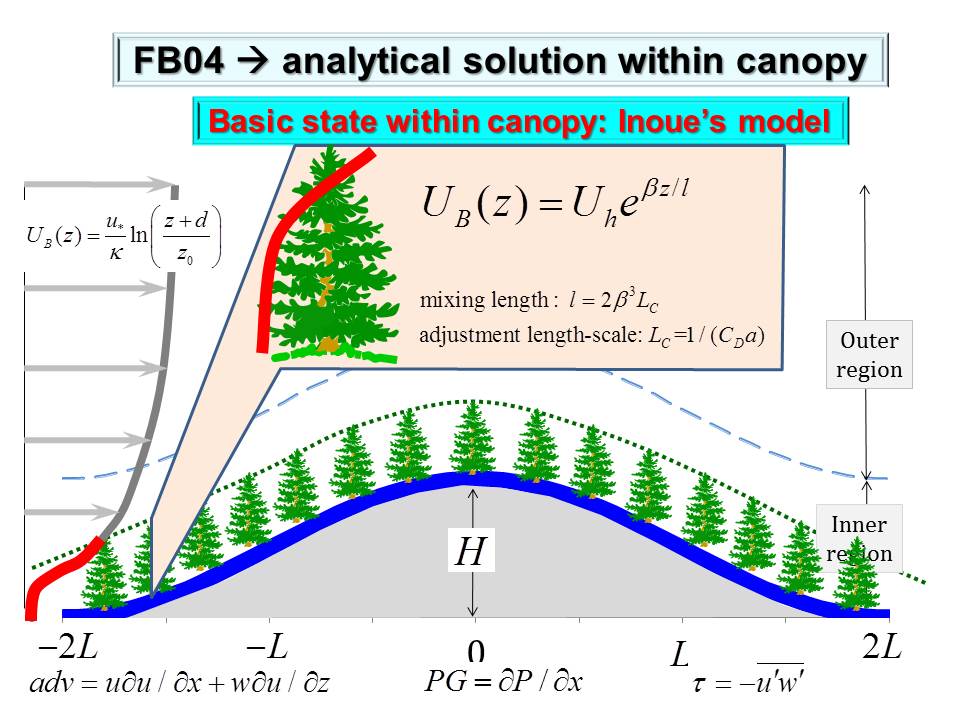
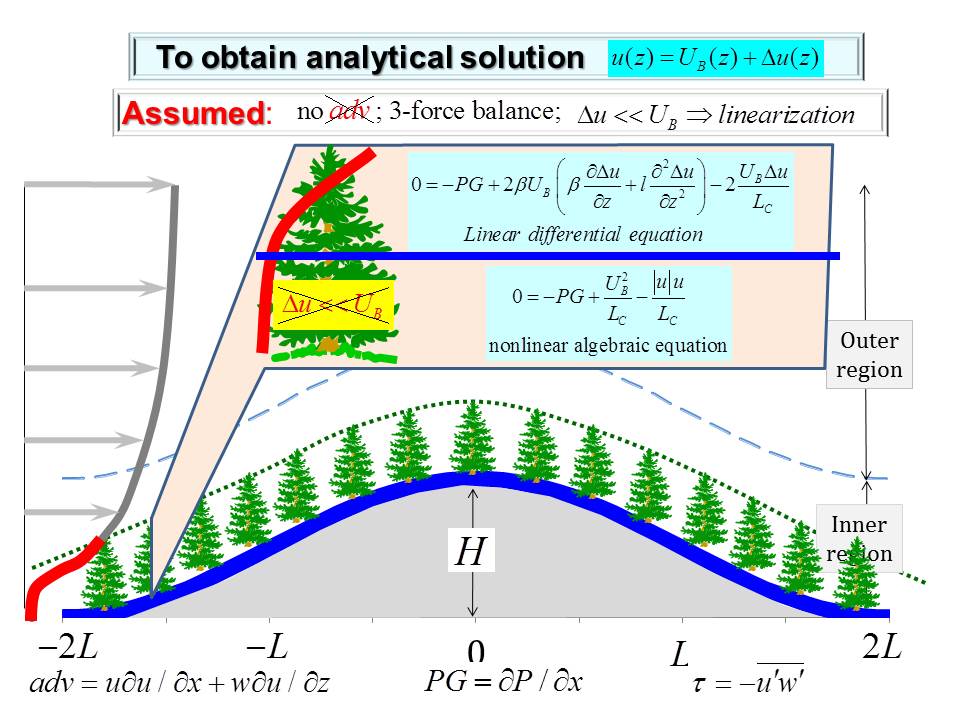
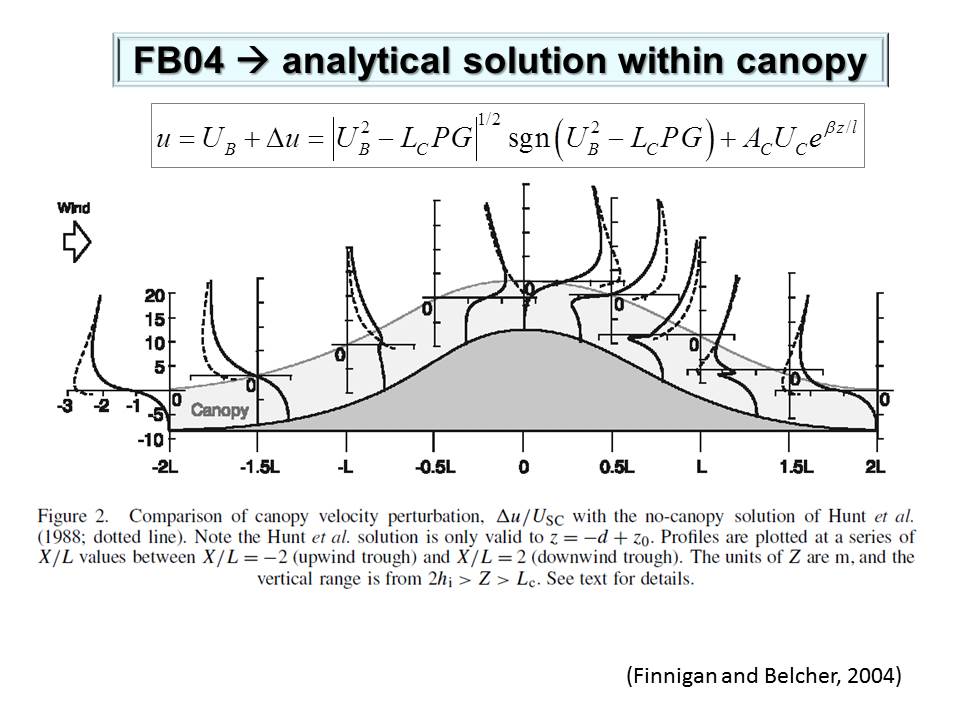
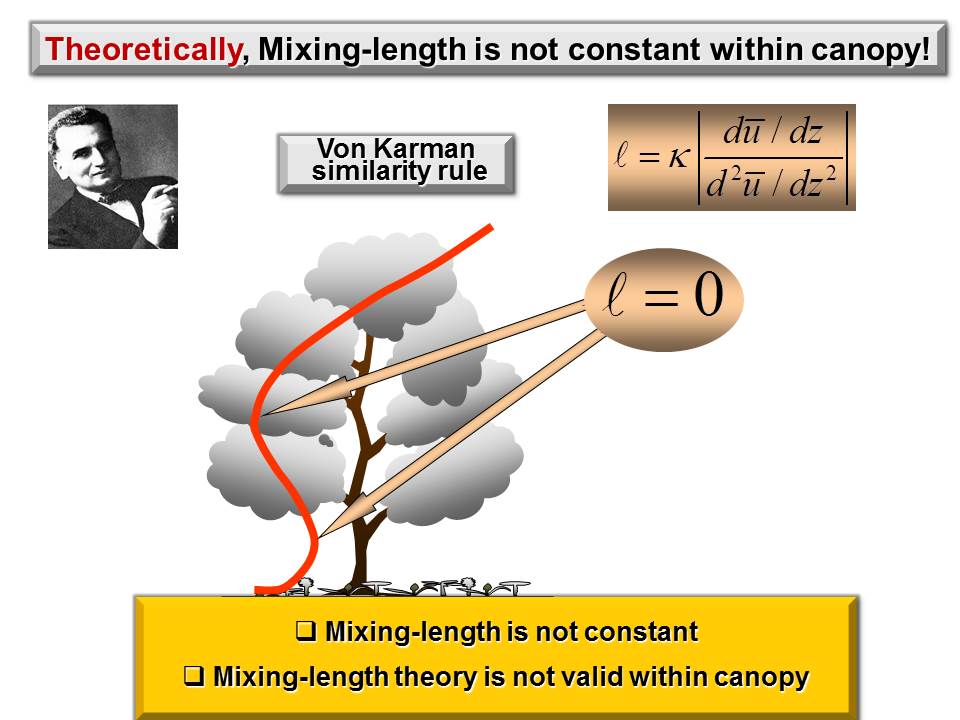
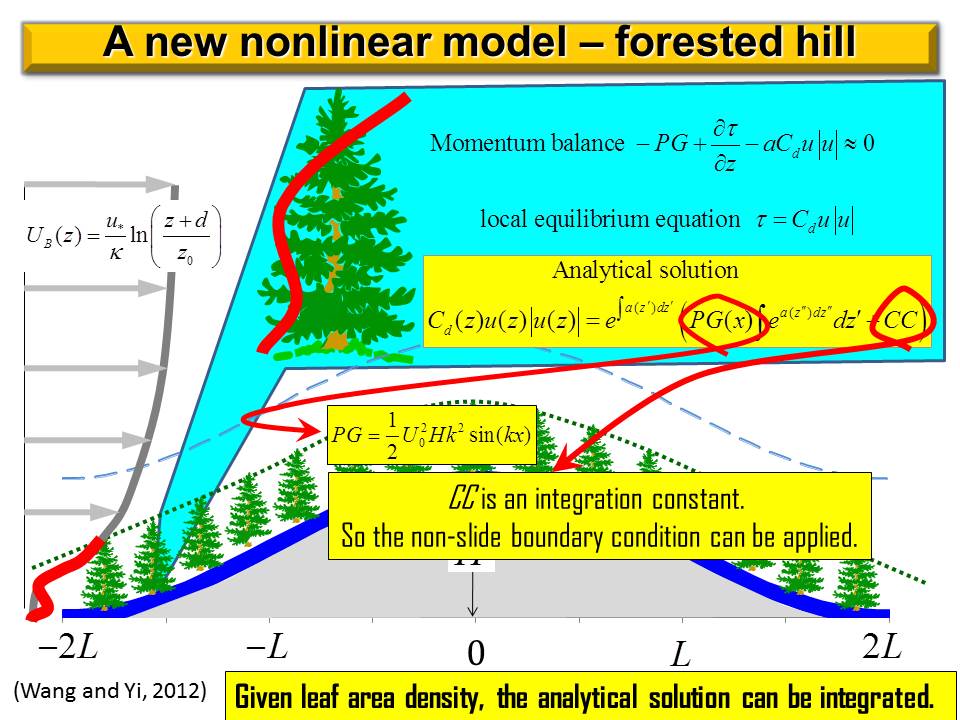
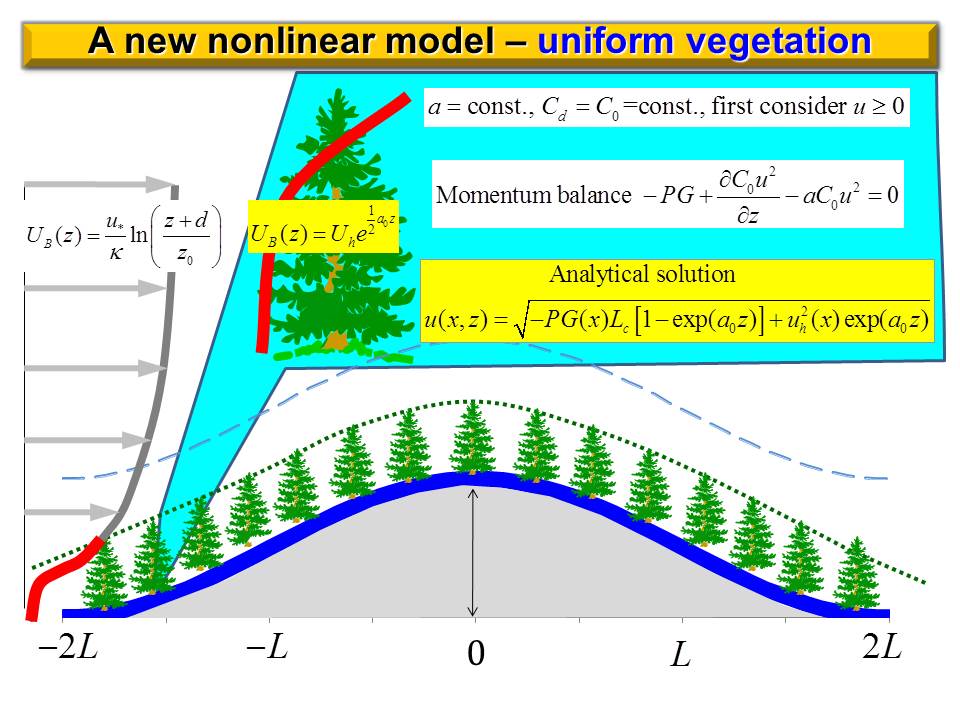
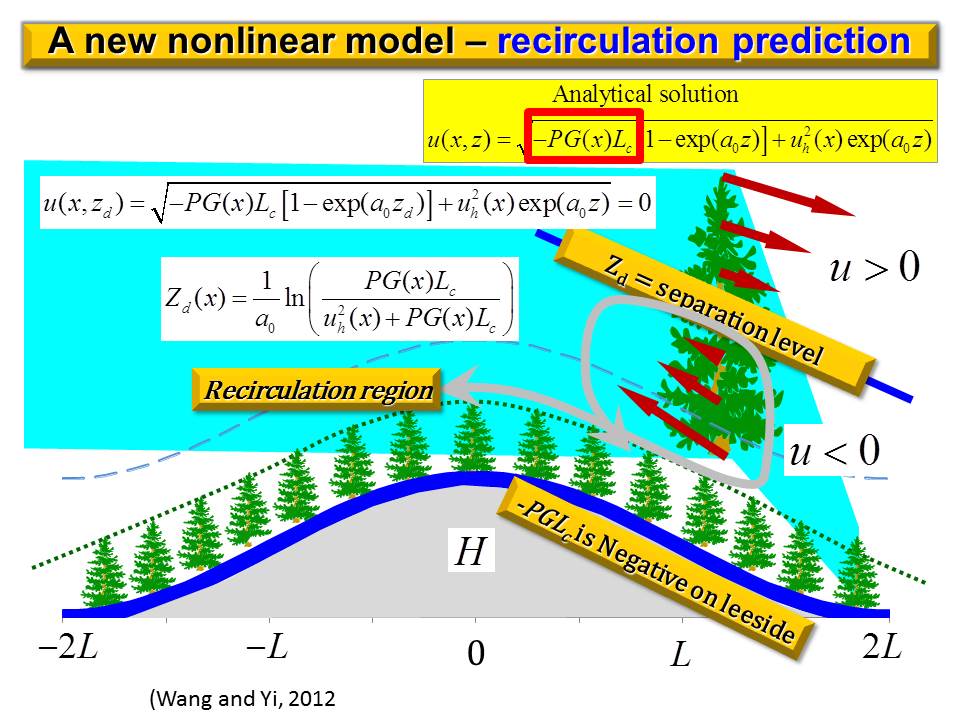
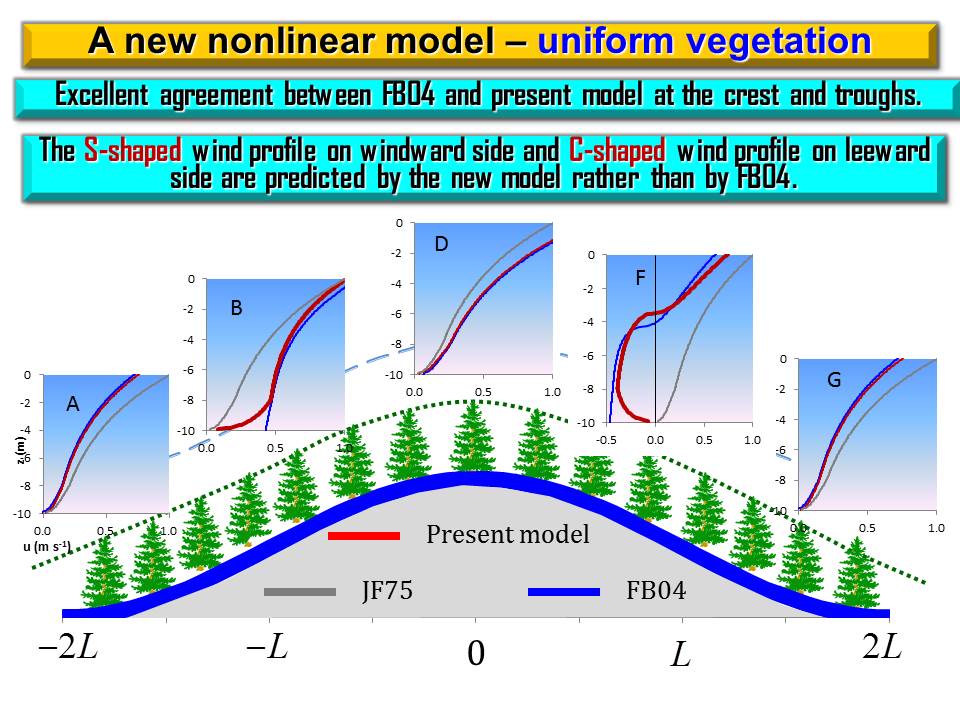
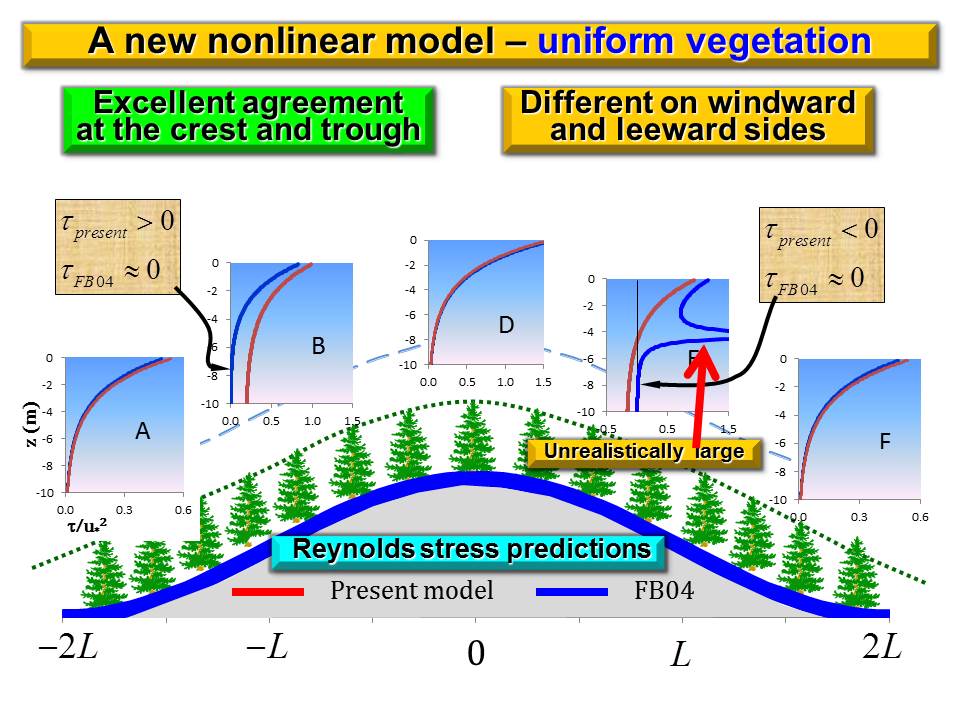
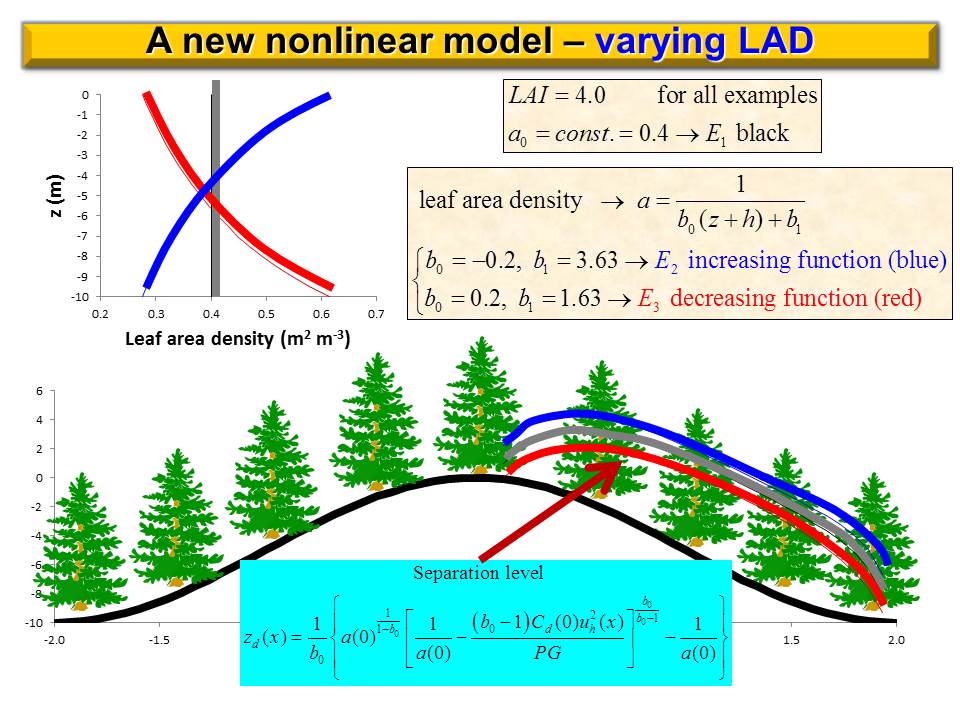
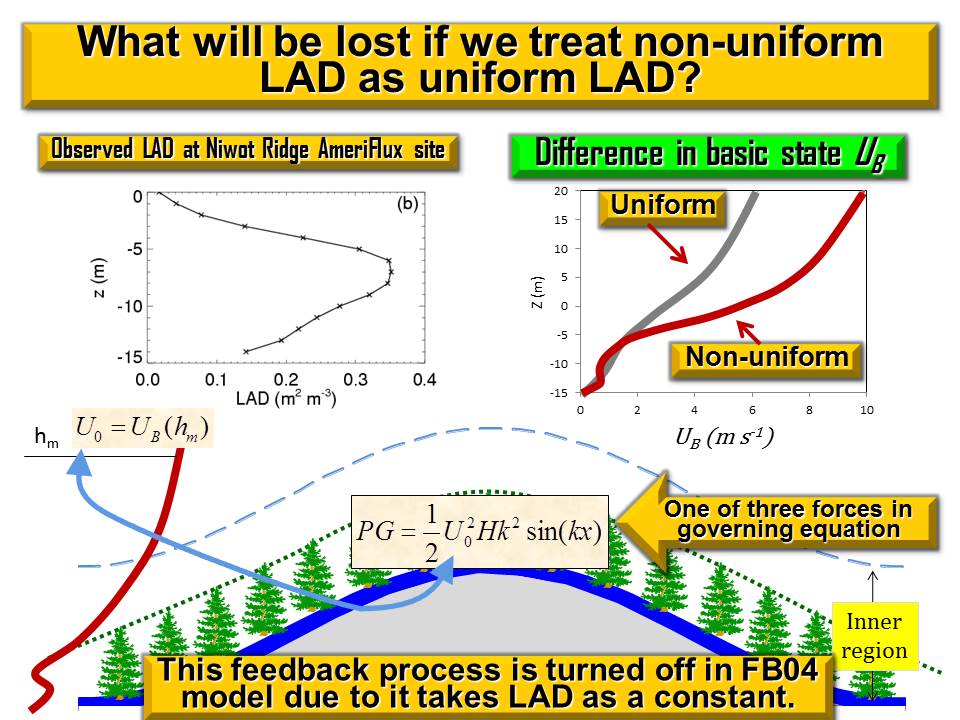
Here we present a nonlinear canopy model that can be used to analytically study momentum transfer and recirculation occurrence within forest canopy over complex terrain. Compared to the model developed by Finnigan and Belcher (2004), hereafter referred to as FB04, this nonlinear model has many advantages. Canopy flows over a gentle forested hill is described by a single nonlinear differential equation with the balance of three forces: canopy drag; topography-induced pressure gradient; and turbulent stress gradient. This nonlinear differential equation is closed by using the local equilibrium relationship as a parameterization scheme. The physical inconsistency generated by applying mixing-length theory in FB04 model is avoided. A non-slip boundary layer condition can be applied to the nonlinear differential equation in our model but cannot be applied to the nonlinear algebraic equation in FB04 model. Our model predicts that wind profile is S-shaped on windward side and C-shaped on leeward side of a forested hill, while FB04 model predicts that wind speed is almost constant in the lower part of canopy because governing equation is algebraic. This nonlinear model also predicts that a recirculation height is determined basically by three factors: lead area density (LAD), the cascade dissipation of kinetic energy at the top of canopy, and work done by perturbation pressure gradient on canopy length scale. An interesting prediction of this nonlinear model is that varying LAD affects the wind profile not only directly but indirectly through a feedback process. Varying LAD has a large impact on background wind distribution, particularly on the characteristic wind velocity in the outer region and hence changing perturbation pressure gradient in the inner region. Thus, wind speed of canopy flows is indirectly changed through this feedback process. In FB04 model, this feedback process is turned off because LAD is assumed to be constant.